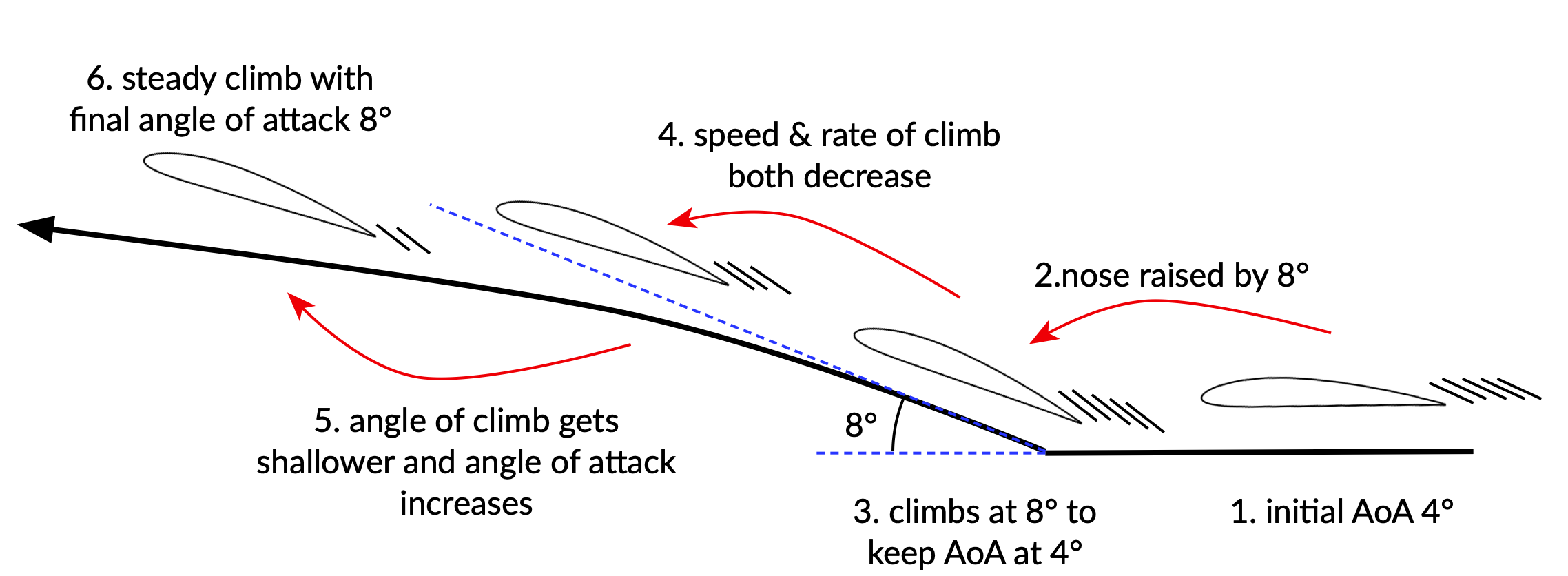
THIS POST is prompted by someone who asked me recently that they wanted a more intuitive understanding of the concept of Angle of Attack from the perspective of the pilot. That can be a big ask; I think many very competent pilots have only a vague idea about angle of attack and “flying the wing” and they seem to manage very well. You can have a lot of skill at all sorts of manoenuvres and not really “get” the idea of Angle of Attack, but I think flying is more fun if you do.

So I thought it would be interesting to discuss using ideas of Angle of Attack and some basic physics why, for instance, when you pull back on the yoke an airplane will enter a climb, and how that climb changes from and settles down. For clarity I’m talking about an airplane in regular cruise flight, not one close to a stall. Nothing tricksy or complicated here, just a manoeuvre that’s taught (that I teach) in the very first flying lesson to a new student.

One of the difficulties in understanding this is that we are all very familiar with a different mode of transport – the motor car. A car follows the road or path that it’s on; if the road goes uphill then the car enters a climb as it goes along the road, and, at the same time, it points uphill too: its pitch changes nose-up. So intuitively we feel that anything that points uphill should go uphill too. If you’re looking for more confirmation then think of a firework rocket: a rocket points uphill and then flies uphill, so isn’t that all an airplane is doing?

Well, not really. Oftentimes an airplane can point uphill but be descending. Or, point uphill and go in level flight. (Maybe lessons three and four of flying!). So there’s clearly something to be explained.

Let’s go back to to the airplane in level (cruise) flight. If the flight is steady, then all the forces on the airplane are in balance. If we label the forces as thrust, weight, lift and drag, they all add up (in a ‘vector’ sense) to zero. That’s lesson one of pilot ground-school aerodynamics.

Let’s pull back on the yoke and examine what happens next.

When we move the yoke we upset the pitch balance of the aircraft, in order to rotate it either nose up or nose down. Another time I’m going to write about pitch stability, and how the elevator controls pitch. But, intuitively we know that in normal flight we can select and control a new pitch attitude by moving the elevator to the appropriate position. Let’s jump ahead a fraction of a second to immediately after we’ve done that.

So far so good: we have changed the pitch angle of the aircraft, but nothing else, yet.

However, by rotating the whole aircraft we are now presenting the wing to the airflow at a different angle: the direction the airplane is moving hasn’t changed, and nor has its airspeed, but its attitude is nose-high compared to previously. So the Angle of Attack of the wing has increased.

That means the amount of lift generated by the wing has increased.

Now the vertical forces are out of balance so the plane starts to accelerate upwards. It starts to climb, and to climb at an increasing rate.

An increasing rate of climb can’t go on for very long: even a modest vertical acceleration would result in an enormous climb rate – thousands and thousands of feet per minute – if left unchecked for long enough. We know from experience that’s not what happens.

As the aircraft starts to climb, the direction of the relative airflow changes: the airplane is moving upwards but with the same attitude, so the relative airflow arrives more from on top of the airplane: this means there’s a decrease in the angle of attack of the wing: as the vertical speed increases – as the airplane climbs faster and faster – the lift produced by the wing goes down. The rate at which the rate of climb increases (a rate of increase in a rate of climb is an acceleration) diminishes. Once the force has decreased to the point where the forces have balanced again the rate of climb becomes steady.

Note this process (to this point) happens quite quickly: in a second or two. In this time the airplane hasn’t had a chance to climb very far, and its airspeed hasn’t changed, either. It is climbing – but has hardly climbed, yet.

So far what has happened is that the Angle of Attack went suddenly up as we raised the nose, and then the Angle of Attack went quickly back down again as the airplane began a climb into the air above it.

Let’s put some realistic numbers down: Let’s suppose you were in cruise flight at a speed of 110kts and your effective angle of attack¹ was 4°

Let’s suppose that you raised the nose from level flight by 8 degrees. The Angle of Attack increased suddenly from 4° to 12°. After a second – when the rate of climb has peaked and the speed has not yet slowed – you might expect a rate of climb of about 1500 feet per minute, which would be exactly enough to reduce the angle of attack back down by 8 degrees – putting it back to 4° where it was in cruise. The vertical forces are pretty much back in balance.

What happens next? Your experience should tell you that two changes happen over the next ten or twenty seconds. Firstly the airspeed decays. Secondly the rate of climb goes down too.

Immediately after raising the nose from cruise a lightly powered training airplane can climb at more than a thousand feet per minute. This is sometimes described as a zoom climb, or an upwards balloon. In energetic terms the plane is trading kinetic energy (airspeed) for height energy (climbing against gravity), just like when you throw a ball upwards.

Although, with the same angle of attack as previously, the forces are almost in balance, they’re only almost in balance. The airplane slows (slowly!) and the rate of climb decreases, slowly. After some seconds we end up in a steady climb at a reduced airspeed, and climbing at a much slower rate than in that first hopeful second or two of zoom-climb.

By how much does the airspeed decrease? And what is the eventual long-term rate of climb? You could use the graphical method from here to try to understand that, and from the point of view of balancing the forces, to see why it’s helpful to add as much thrust as possible in a climb.

However let’s simplify. We’ll keep our 8° nose up attitude, and add enough power (thrust) to stabilize the airspeed at 80 knots, for example.

Even at this pitch attitude very little engine thrust acts vertically to support the weight of the aircraft, and the climb angle is shallow enough that there’s no vertical component of drag: so to a good approximation, the lift remains equal to the weight, just as it was in level cruise flight.

A little arithmetic will give us our final rate of climb: a reduction in speed from 110 in cruse to 80 in climb reduces lift by a factor of (8/11) squared² which is very close to 50%. So compared to cruise we need to double the Angle of Attack to maintain equilibrium, bringing the Angle of Attack from 4° to 8°.³

If the airplane is pointed 12° nose up, but has an 8° Angle of Attack, it must actually be climbing at a 4° angle. (Angle of attack is the difference between where the airplane is pointing and where it’s going, remember?)

4° angle of climb at 80 knots is a rate of climb of 565 feet per minute – which is pretty much what we would expect from a small training airplane in a sustained climb.

To conclude then, just raising the nose from cruise results in the following Angle of Attack changes:

1. A sudden increase as you raise the nose
2. An almost-as-sudden decrease as the aircraft enters a zoom climb
3. A gentle increase as the rate of climb decreases and the aircraft slows down
4. A new steady value, higher than in cruise, because of the reduced airspeed.

1. Zero effective AoA is the direction the wing moves into the relative wind to generate zero lift.
2. The lift equation tells us that lift depends linearly on effective angle of attack, until close to the stall, and on the square of the airspeed.
3. For clarity, this value of 8° is not related to the 8° we raised the nose, initially – that’s just how the numbers worked out.