Here’s a post for people interested in basic aerodynamics.

Imagine you’re in a small airplane in level flight at 100 knots. You increase power and pitch up to place the aircraft in a climb, at the same airspeed, 100 knots. Has the angle of attack increased, stayed the same, or decreased? Has the load on the wing increased or decreased?

Have a think about your gut instinct before you read the rest.

The four forces of flight

Here’s a way to determine the answer, without doing lots of maths. Let’s review the four forces of flight: lift, weight, thrust, and drag. Weight (W) is the mass of the airplane, acted upon by gravity – it always acts downwards. Thrust (T) is the force produced by the engine or engines. Let’s presume it acts backwards in the direction the engines are facing.

Lift (L) and drag (D) are the interesting ones – they’re the aerodynamic forces produced by the wings and other parts of the aircraft being pressed on by the air. Pilots are familiar with the idea that the drag acts against and in the same direction to the direction of the relative airflow (the direction the airplane is actually moving through the air) while lift is the force at right angles to the direction of motion. So lift and drag are always at right angles to each other.

Let’s turn to every pilots favourite aerodynamics text Theory of Flight by Richard Von Mises.

Figure 98 gives a typical graph of L vs D for a wing at different angles of attack. More accurately, the figure is a plot of the coefficient of lift vs the coefficient of drag (C_L vs C_D), both of which are dimensionless quantities removing the dependence of the actual lift and drag on air density, velocity, wing area and so on. but showing how lift and drag vary with angle of attack α.

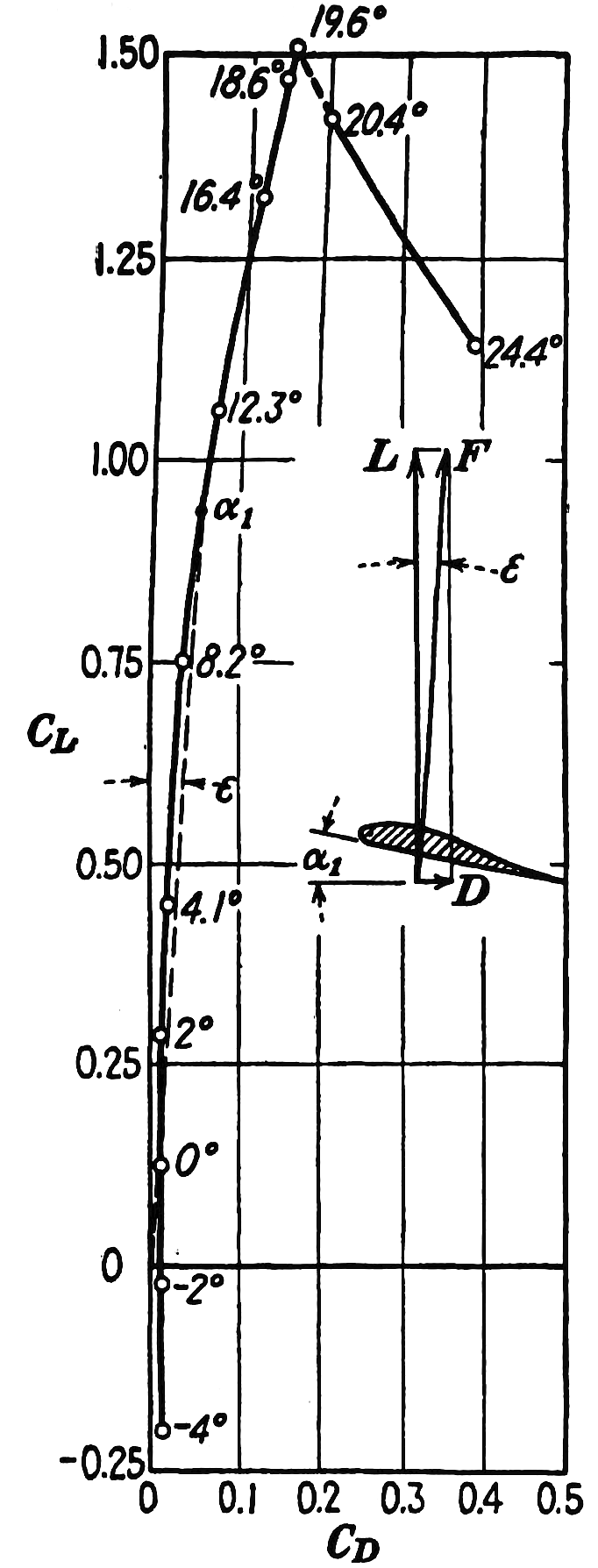
As Von Mises points out, the actual force provided by the wing F, is the combination of L and D: the genius of the wing is that it generates a large upward force L if you can overcome only a small backwards force D.

We can add the third of four forces, thrust (T) to the same diagram, reasoning as follows: let’s make the assumption that the engine provides thrust parallel to the chord line of the wing. That is, the engine is horizontal when the wing is “horizontal”.

The angle between the relative airflow and the chord is the angle of attack α, and T is parallel to the chord, so T also is at α degrees to the relative airflow, and so T is at α degrees to D, and since D is along the x axis, T makes an angle to the x axis that is the same as the angle of the attack of the airplane.

Since the curve in Fig.98 is parameterized by α, we can add to figure 98 a family of lines representing possible thrust directions, each making an angle to the X axis the same as the value of α at which it meets the L-D curve. The length of the green arrow represents the magnitude of the thrust.

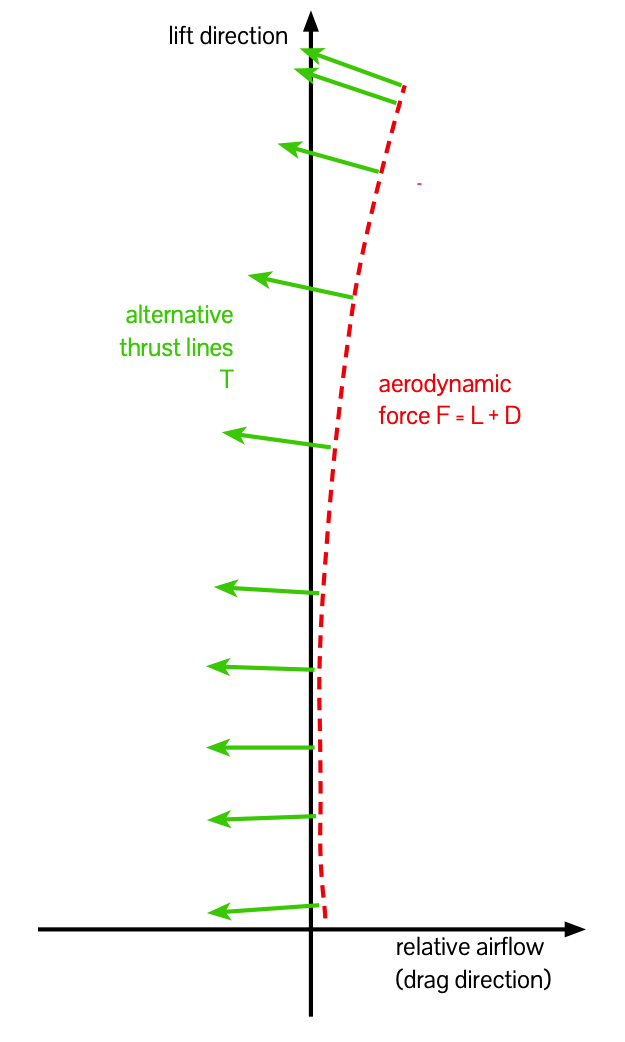
Next, we’re going to add some extra drag to represent the increased parasite drag of the whole airplane, compared to just the wing:

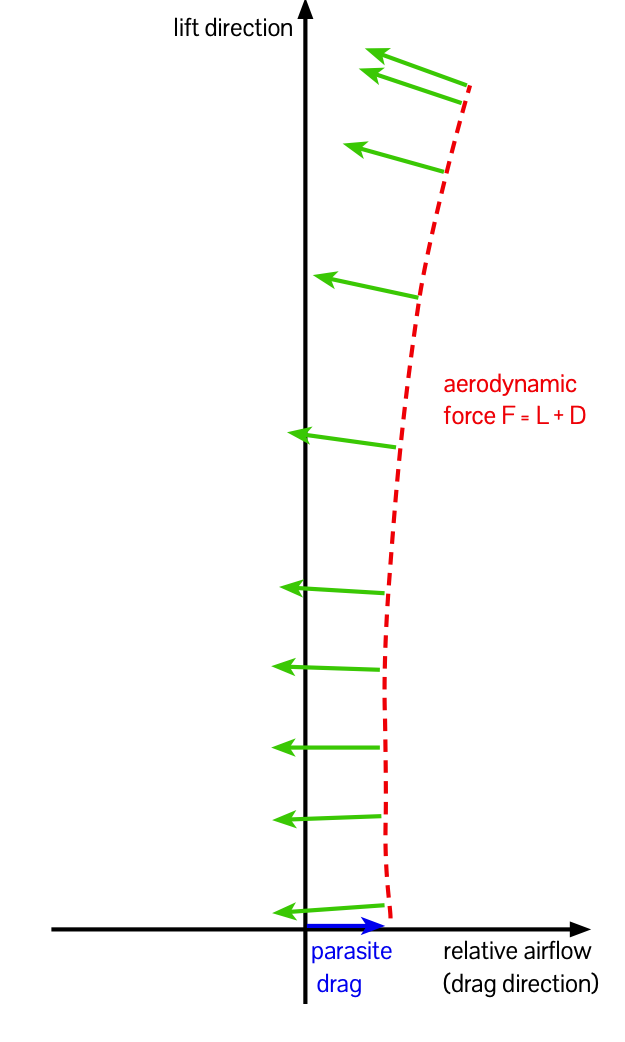
Finally we consider the last of the four forces: weight (W). With the airplane in equilibrium all the forces are in balance and sum to zero, so we can write a (vector) equation F + W + T = 0, or, if we represent each force as an arrow and put them head-to-tail they make a closed triangle figure:

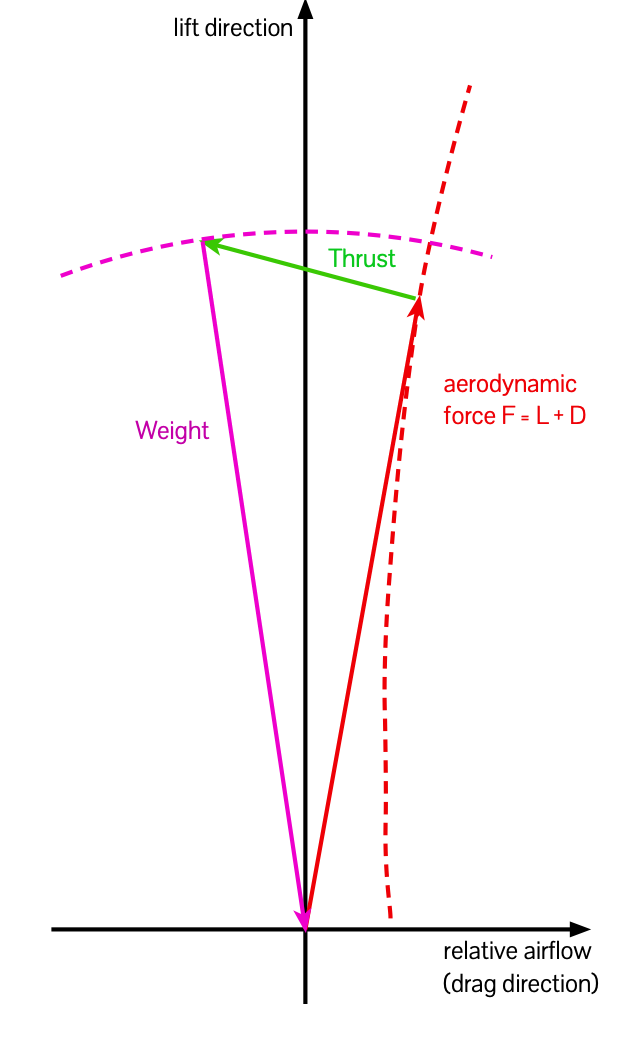
Given the graphical representation of F (which is L + D) we added T, and now we know W closes the shape, so for any angle of attack and thrust, W can be only one value, fixed by joining the end of the selected T back to the origin.

Now one of the things we know about weight is that it always acts vertically downwards. To see what’s going on, if W isn’t vertical, we should rotate the entire graph, axes and all, until it is.

And when we do that, it becomes pretty obvious that the direction of D (which is opposite to the direction the plane is moving) shows the plane either climbing or descending.

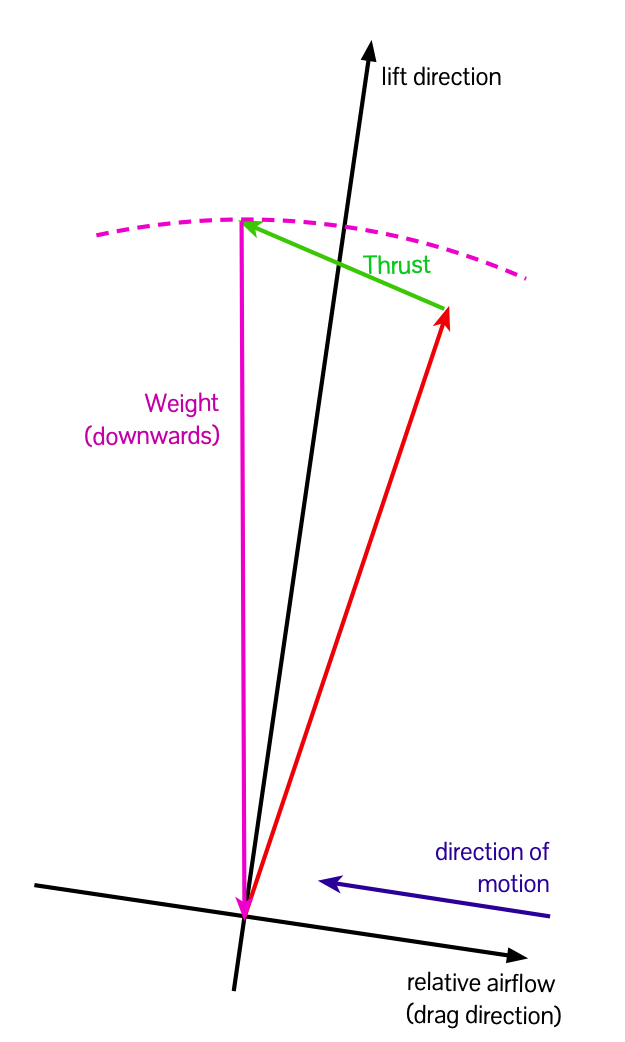
It’s rather tedious to do that each time, but going back a step, it should be clear that if the end of F + T is to the left of the vertical axis, then the aircraft ends up in a climb, if F + T ends on the vertical axis, the aircraft is in level flight, and if F + T ends up to the right of the vertical axis, the aircraft is in a descent.

Going back to our puzzle then: We start with the airplane in equilibrium in level flight. So F + T ends on the vertical axis, and W is vertical. Adding thrust from T to the longer T’, and noting the weight stays the same, so W and W’ are the same length, that means that F becomes shorter, the load on the wing decreases, and the point at which T meets F represents a lower angle of attack.

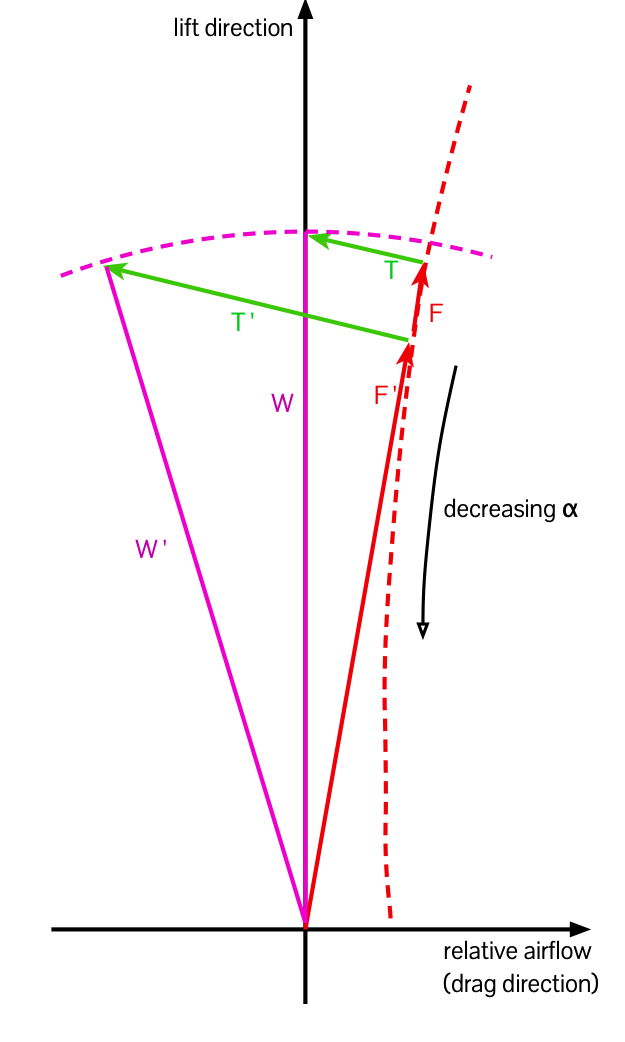
In other words, compared to level flight, when climbing at the same airspeed the angle of attack has decreased, and the force on the wing is decreased. Is that what you expected?