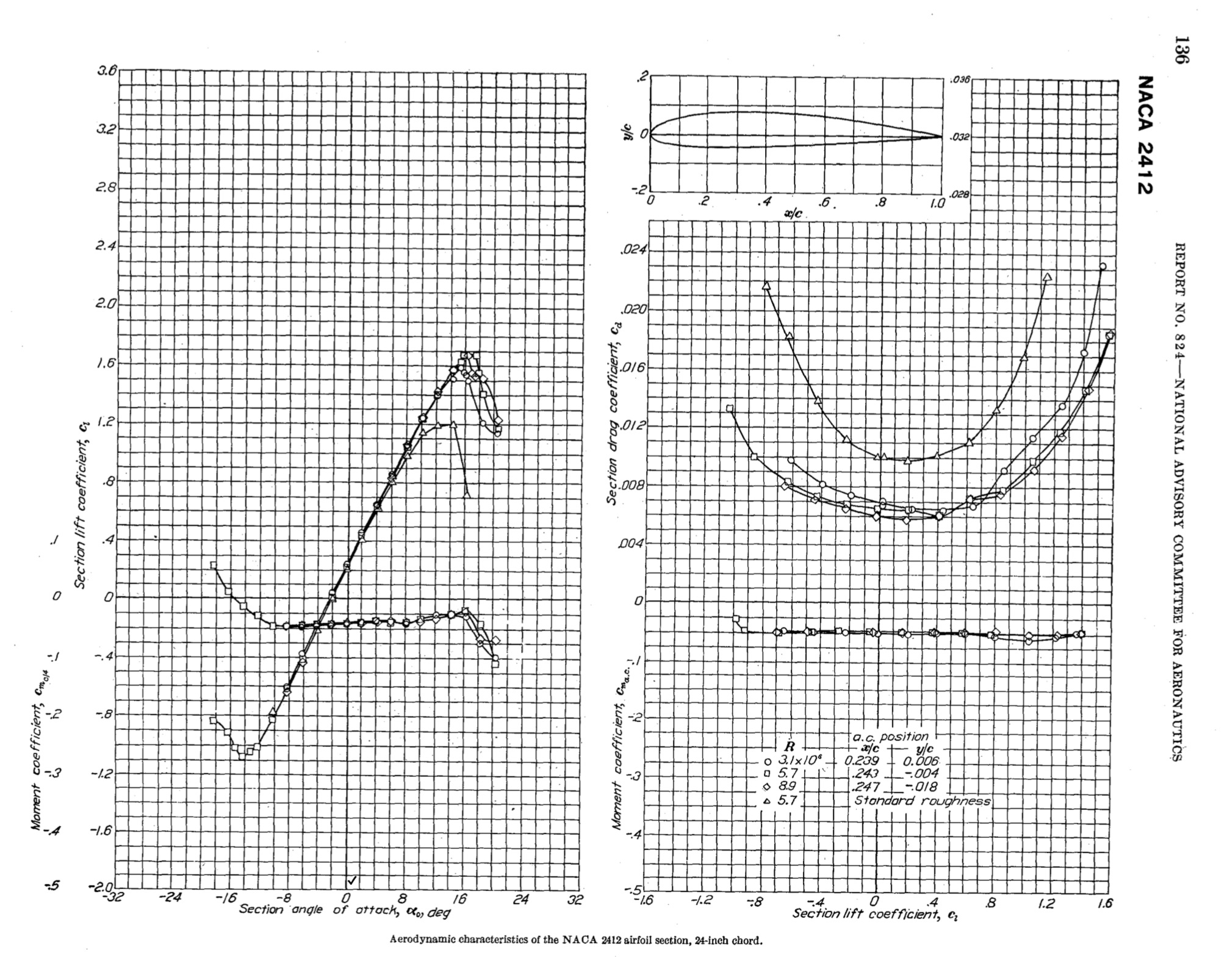
A friend asked me to estimate the force exerted by the tailplane on the fuselage of a Cessna 182, this week. In the course of answering I located and/or worked out some information that might interest you.

Dynamic pressure vs. atmospheric pressure

Firstly – at 100 knots at sea level, the dynamic pressure is 34 lbs (force) per square foot. (If you stick your hand out of the window into the slipstream, that’s the pressure you’d feel against it.) You can work this out from the air density, and the air speed.

By contrast, atmospheric pressure at sea level is 2116 lbs per square foot. So the dynamic pressure is only 1.6% of atmospheric pressure. Of course atmospheric pressure is exerted on both sides of every surface, so it has no net effect. Whereas the dynamic pressure, or small multiples of it, works differently between the top surface and the bottom surface of the wing, which is what lifts and holds the airplane up in the air.

Wing loading and coefficient of lift

Secondly: with a maximum weight of 2950 lbs, and a wing area of 172 square feet, the load per square foot for the C182 wing in steady flight is 17 lbs per square foot.

When a wing generates lift, the ratio of the lift per square foot to the dynamic pressure has a special name: we call it the coefficient of lift (C_l) which depends on the angle of attack of the wing (α), the angle at which the wing meets the airflow.

So the value of C_l required, at 100kts, and at maximum gross weight, for the C182, is close to exactly 0.5 (17 divided by 34).

C_l and c_l

The 182 wing has a NACA 2412 airfoil, the data for which, you’ll find on page 136 of this document. The left side of the page gives a graph of “section coefficient of lift” c_l (vertical axis) against α (horizontal axis). I’ve included the page in this post, at the top.

What’s the difference between coefficient of lift C_l and section coefficent of lift c_l? C_l (with the capital letter) applies to a whole wing, and so includes spanwise effects – especially the airflow at and around the wingtips. On the other hand c_l is what you’d get if the flow were just two dimensional, or equivalently, if the wing were infinitely long. It ignores what happens around the wing tips. It’s approximately the same as C_l if the wing has a high enough aspect ratio. The Cessna 182 wing has an aspect ratio of 7 to 1, so we will imagine this is long enough to represent the whole-wing coefficient of lift by the section coefficient of lift of its airfoil section.

Angle of attack

From the NACA data, you can see that the α needed to give a c_l of 0.5 (and approximaetly a C_l) is 2°. The AoA of the NACA 2412 airfoil that generates zero lift is -2°, so at 100 knots, α is +4° above the zero-lift angle.

Tailplane force

The corresponding coefficient of lift of the tailplane could be anywhere from about -2 to +2. With horizontal stabilizer area of about 40 sq. feet, the tailplane force could be anything up to 3200 lbs. Does that seem rather high? Is the tailplane structure strong enough to bear that sort of load without damage? If you’re not sure the answer is yes then it might be a good idea to avoid making abrupt or full-deflection elevator inputs at anything faster than fairly slow airspeeds.